莫队算法

用于解决一类区间询问问题的办法

对于一段给定的数据序列，有 $m$ 次询问，询问的区间 $[l,r]$ 如果能够在 $O(1)$ 的时间复杂度内将区间拓展到 $[l\pm1,r\pm 1]$ ，那么我们就能够在 $O(n\sqrt n)$ 的时间复杂度内计算所有询问的答案

将这段数据序列均匀划分为 $\sqrt n$ 个区域，对所有的询问离线后按照 $l$ 块的编号，$r$ 块的编号进行双关键字排序

以洛谷 P2709 为例：

题目描述

小B 有一个长为 $n$ 的整数序列 $a$，值域为 $[1,k]$。
他一共有 $m$ 个询问，每个询问给定一个区间 $[l,r]$，求：$$\sum\limits_{i=1}^k c_i^2$$ ，其中 $c_i$ 表示数字 $i$ 在 $[l,r]$ 中的出现次数。

struct que{
    int l,r,id;
};

void solve(){
    int n,m,k;
    cin>>n>>m>>k;
    vector<int> a(n+1);
    for (int i=1;i<=n;i++) cin>>a[i];
    vector<que> q(m);
    for (int i=0;i<m;i++) cin>>q[i].l>>q[i].r,q[i].id=i;
    int B=sqrt(n);//分块大小
    vector<int> cnt(n+1);
    LL sum=0;
    
    auto cmp=[&](que x,que y){
        if (x.l/B==y.l/B) return x.r<y.r;
        return x.l<y.l;
    };//双关键字排序
    
    auto add=[&](int x){
        sum-=cnt[a]*cnt[a];
        cnt[a]++;
        sum+=cnt[a]*cnt[a];
        
    };
    auto del=[&](int x){
        sum-=cnt[a]*cnt[a];
        cnt[a]--;
        sum+=cnt[a]*cnt[a];
    };
    sort(q.begin(),q.end(),cmp);
    vector<int> ans(m);
    for (int i=0,l=1,r=0;i<m;i++){
        while (l>q[i].l) add(--l);
        while (r<q[i].r) add(++r);
        while (l<q[i].l) del(l++);
        while (r>q[i].r) del(r--);
        ans[q[i].id]=sum;
    }
    for (auto x:ans) cout<<x<<endl;
}

特别的，朴素的莫队算法常数比较大，原因有一部分是因为在相同块内的 $r$ 指针都是单调排列的，在相邻块间移动时 $r$ 指针前后会重复移动：

image-20250806224156020

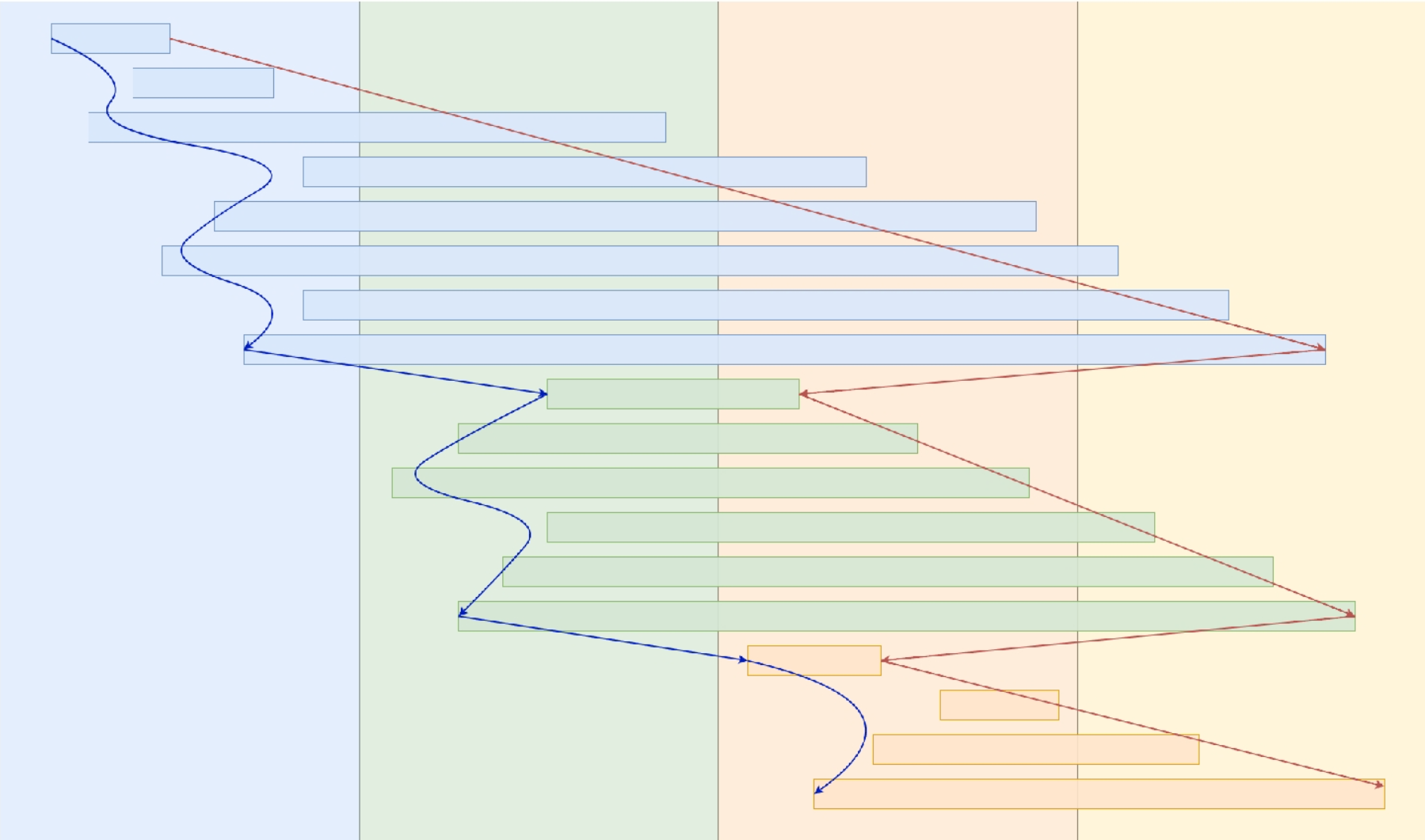
解决办法时将奇数块的内的 $r$ 按照升序排列，偶数块内的 $r$ 按照降序排列：

image-20250806224259805

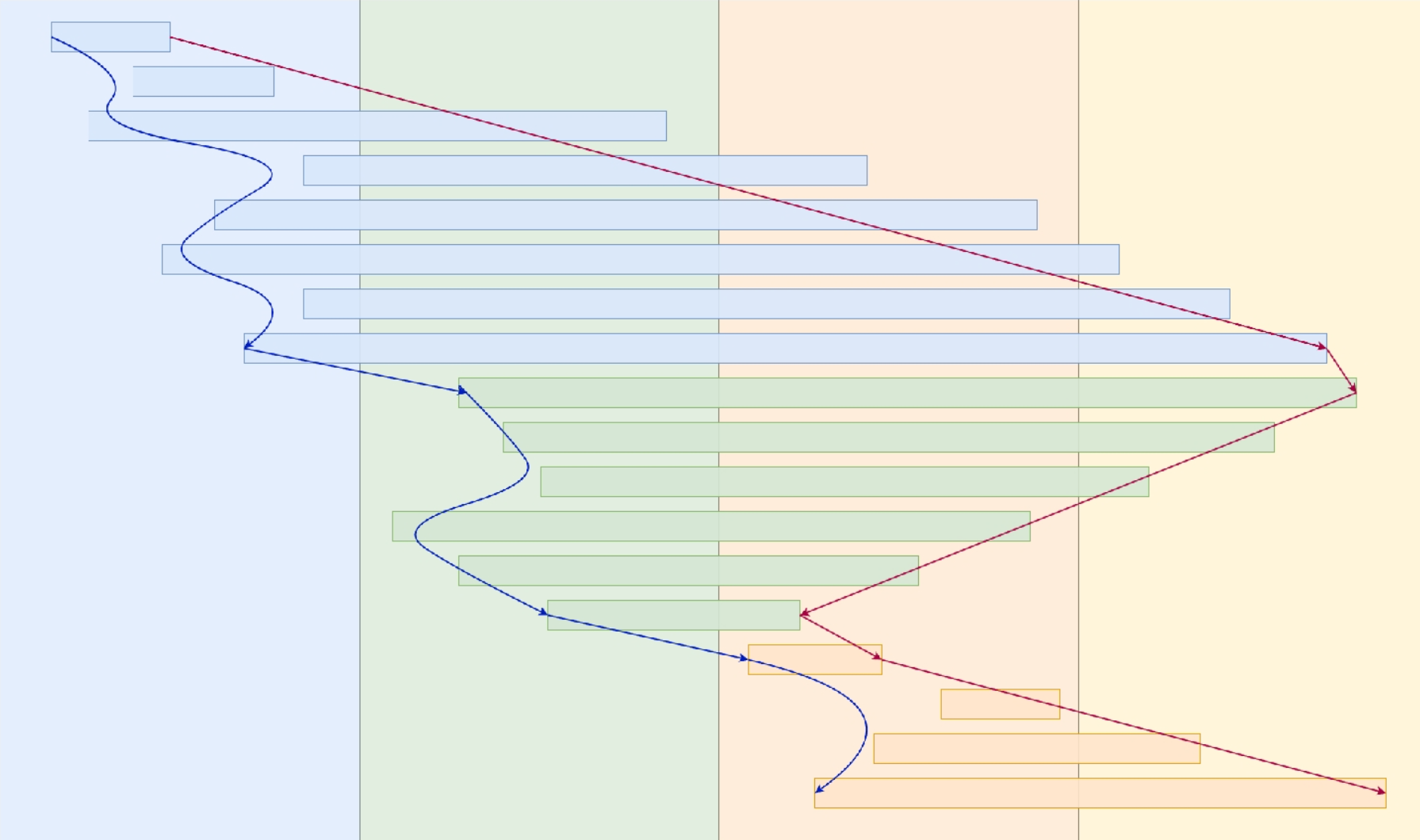
auto cmp=[&](que x,que y){
    if (x.l/B==y.l/B) return (x.l/B&1)?x.r<y.r:x.r>y.r;
    return x.l<y.l;
};//双关键字排序

带修改莫队

一般情况下，对于区间查询问题莫队算法可以有良好的时间复杂度，但是如果需要执行区间修改操作，那么普通的莫队算法就不能维护出区间的信息

我们对所有操作都记录下它的时间戳，按照三关键字进行排序后，两个询问之间的时间差为 $tim_i-tim_j$

只要能够在时间复杂度可接受的（$k=O(1),O(\log n)$) 范围内维护出这段时间差中的贡献，那么就可以做到 $O(n^{\frac{5}{3}}\times k)$ 的时间复杂度回答

以洛谷 P1903 为例

题目描述

墨墨购买了一套 $N$ 支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。墨墨会向你发布如下指令：

  1. $Q\ L\ R$ 代表询问你从第 $L$ 支画笔到第 $R$ 支画笔中共有几种不同颜色的画笔。
  2. $R\ P\ C$ 把第 $P$ 支画笔替换为颜色 $C$。

为了满足墨墨的要求，你知道你需要干什么了吗？

struct que{
    int l,r,id,tim;
};

void solve(){
    int n,m;
    cin>>n>>m;
    vector<int> a(n+1);
    for (int i=1;i<=n;i++) cin>>a[i];
    vector<que> q(m+1);
    vector<pair<int,int>> R(m+1);
    int id=0,tim=0;
    for (int i=0;i<m;i++){
        char c;
        int l,r;
        cin>>c>>l>>r;
        if (c=='Q') q[++id]={l,r,id,tim};
        else R[++tim]={l,r};
    }
    
    int B=pow(n,0.666);
    
    auto cmp=[&](que x,que y){
        if (x.l/B!=y.l/B) return x.l<y.l;
        if (x.r/B!=y.r/B) return (x.l/B&1)?x.r<y.r:x.r>y.r;
        return x.tim<y.tim;
    };
    
    sort(q.begin()+1,q.begin()+id,cmp);
    
    vector<int> mp(1000010);
    int sum=0;
    vector<int> ans(id+1);
    
    auto add=[&](int x){
        if (++mp==1) sum++;
    };
    
    auto del=[&](int x){
        if (--mp==0) sum--;
    };
    
    for (int i=1,l=1,r=0,tim=0;i<=id;i++){
        while (l>q[i].l) add(a[--l]);
        while (r<q[i].r) add(a[++r]);
        while (l<q[i].l) del(a[l++]);
        while (r>q[i].r) del(a[r--]);
        while (tim<q[i].tim){
            tim++;
            int p=R[tim].first;
            if (l<=p&&p<=r) del(a[p]),add(R[tim].second);
            swap(a[p],R[tim].second);
        }
        while (tim>q[i].tim){
            int p=R[tim].first;
            if (l<=p&&p<=r) del(a[p]),add(R[tim].second);
            swap(a[p],R[tim].second);
            tim--;
        }
        ans[q[i].id]=sum;
    }
    for (int i=1;i<=id;i++) cout<<ans[i]<<endl;
}

可以证明这种情况下将分块大小设置为 $n^{\frac{2}{3}}$ 是最优的，对于每个新扩展进来的元素，我们可以 $O(1)$ 的统计是不是一个没有出现过的元素，所以总的时间复杂度为 $O(n^{\frac{5}{3}})$

对于一段当前询问的区间以及它的时间戳 $tim_i$ ，维护出当前时间戳 $x$ 到这段时间中修改操作的贡献

while (tim<q[i].tim){
    tim++;
    int p=R[tim].first;
    if (l<=p&&p<=r) del(a[p]),add(R[tim].second);
    swap(a[p],R[tim].second);
}
while (tim>q[i].tim){
    int p=R[tim].first;
    if (l<=p&&p<=r) del(a[p]),add(R[tim].second);
    swap(a[p],R[tim].second);
    tim--;
}