ST表

ST表（Sparse Table，稀疏表）

主要用来解决 RMQ，可重复贡献问题 问题，相比于线段树，ST表能够做到在 $O(n\log n)$ 的时间内预处理，以 $O(1)$ 的速度查询

基于倍增算法，预处理每个区间，这里以维护区间最大值为例

原理是利用倍增法递推，用两个等长的小区间拼凑大区间

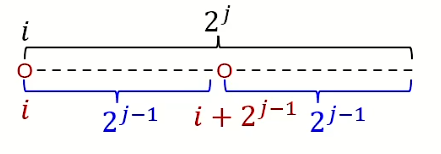
记 $f_{i,j} $ 为以 $a_i$ 为左端点，区间长度为 $2^j$ 的区间中的最大值，那么满足递推式

$$ f_{i,j}=max(f_{i,j-1},f_{i+2^{j-1},j-1}) $$

for (int i=1;i<=n;i++) f[i][0]=a[i];
for (int j=1;j<=maxlg;j++)//maxlg表示不大于n的最大2次幂的指数
    for (int i=1;i+(1<<j)-1<=n;i++)
        f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); 

$f_{i,j}$ 中第二维 $j$ 的大小通过 $\log_2n$ 计算，可以增加记忆数组 $lg_{i}$ ，用来存储区间长度（速度可能比 log() 快？）

lg[1]=0;
for (int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;//递推计算不大于i的最大2次幂的指数

查询时，从 $[l,r]$ 两端出发，分别延伸出 $lg_{r-l+1}$ 的区间长度，可以证明，这两段一定能覆盖完整个区间

左区间为 $[l,l+2^{lg_{r-l+1}}]$ ，右区间为 $[r-2^{lg_{r-l+1}}+1,r]$

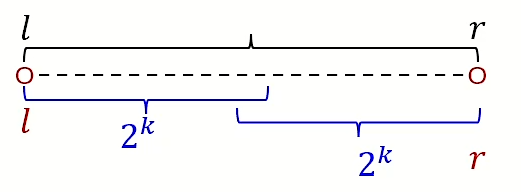
记 $k=lg_{r-l+1}$:

$$ ans=max(f_{l,k},f_{r-2^k+1,k}) $$

cin>>l>>r;
int k=lg[r-l+1];
cout<<max(f[l][k],f[r-(1<<k)+1][k]);//位运算加速

以洛谷P2880为例

 
using namespace std;

int n,q;
int lg[180010];
int f[180010][18];
int p[180010][18];

int main()
{
    cin>>n>>q;
    for (int i=1;i<=n;i++){
        cin>>f[i][0];
        p[i][0]=f[i][0];
    }
    for (int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
    for (int j=1;j<=lg[n];j++){
        for (int i=1;i+(1<<j)-1<=n;i++){
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
            p[i][j]=min(p[i][j-1],p[i+(1<<(j-1))][j-1]);
        }
    }
    while (q--){
        int a,b;
        cin>>a>>b;
        int k=lg[b-a+1];
        cout<<max(f[a][k],f[b-(1<<k)+1][k])-min(p[a][k],p[b-(1<<k)+1][k])<<endl;
    }
    return 0;
}