分层图问题

这里以一道题目为例

题目描述

Alice 和 Bob 现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在 $n$ 个城市设有业务，设这些城市分别标记为 $0$ 到 $n-1$，一共有 $m$ 种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多 $k$ 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少？

输入格式

第一行三个整数 $n,m,k$，分别表示城市数，航线数和免费乘坐次数。

接下来一行两个整数 $s,t$，分别表示他们出行的起点城市编号和终点城市编号。

接下来 $m$ 行，每行三个整数 $a,b,c$，表示存在一种航线，能从城市 $a$ 到达城市 $b$，或从城市 $b$ 到达城市 $a$，价格为 $c$。

输出格式

输出一行一个整数，为最少花费。

样例输入

5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100

样例输出

8

数据规模与约定

对于 $30\%$ 的数据，$2 \le n \le 50$，$1 \le m \le 300$，$k=0$。

对于 $50\%$ 的数据，$2 \le n \le 600$，$1 \le m \le 6\times10^3$，$0 \le k \le 1$。

对于 $100\%$ 的数据，$2 \le n \le 10^4$，$1 \le m \le 5\times 10^4$，$0 \le k \le 10$，$0\le s,t,a,b < n$，$a\ne b$，$0\le c\le 10^3$。

另外存在一组 hack 数据。

区别与一般的单图问题，这道题中我们需要考虑可以免费坐飞机的航线

相当于每个节点都存在一个状态，即到这个节点还能免费坐飞机的次数

拥有相同状态的节点共同组成一张图

所以需要对寻路的方式进行部分修改，这里采用优先队列的Dijkstra最短路算法

struct node
{
    int dw, dnode, cnt;
    bool operator<(const node& a)const {
        return dw > a.dw;
    }
};

构造优先队列 priority_queue 使用的结构体，并重载小于号

其中存储了这个节点的编号dnode ，节点到起始点的距离 dw ，以及当前节点使用的免费次数 cnt

int dis[20010][12];
bool vis[20010][12];

同样的，记录最短距离的 dis 和记录访问节点的 vis 数组都需要根据状态的不同来进行分层操作

void dijkstra(int st) {
    init();
    q.push({ 0, st, 0 });
    dis[st][0] = 0;
    while (q.size())
    {
        const node ttop = q.top();
        q.pop();
        if (vis[ttop.dnode][ttop.cnt]) continue;
        vis[ttop.dnode][ttop.cnt] = 1;
        
        for (auto it = e[ttop.dnode].begin(); it != e[ttop.dnode].end(); it++) {
            if (ttop.cnt < k&& dis[it->v][ttop.cnt + 1] > dis[ttop.dnode][ttop.cnt]) {
                dis[it->v][ttop.cnt + 1] = dis[ttop.dnode][ttop.cnt];
                q.push({ dis[it->v][ttop.cnt + 1],it->v,ttop.cnt + 1 });
            }
            if (dis[it->v][ttop.cnt] > dis[ttop.dnode][ttop.cnt] + it->w) {
                dis[it->v][ttop.cnt] = dis[ttop.dnode][ttop.cnt] + it->w;
                q.push({ dis[it->v][ttop.cnt],it->v,ttop.cnt });
            }
        }
        
    }
}

除了松弛操作外，多层图和单图的源码几乎相同，都采用了优先队列贪心来找当前最优的节点

在松弛操作内，我们需要考虑当前的节点能否使用免费的次数，免费后是不是最优

• 当前的节点可以免费

if (ttop.cnt < k&& dis[it->v][ttop.cnt + 1] > dis[ttop.dnode][ttop.cnt]) {//判断是不是最优
    dis[it->v][ttop.cnt + 1] = dis[ttop.dnode][ttop.cnt];//如果能更新最短路径，那就更新
    q.push({ dis[it->v][ttop.cnt + 1],it->v,ttop.cnt + 1 });//将更新后的节点放入队列，注意状态也要更新
}

• 当前的节点不能免费或不采取免费

if (dis[it->v][ttop.cnt] > dis[ttop.dnode][ttop.cnt] + it->w) {//判断能否更新
    dis[it->v][ttop.cnt] = dis[ttop.dnode][ttop.cnt] + it->w;
    q.push({ dis[it->v][ttop.cnt],it->v,ttop.cnt });//放入更新后的节点
}

Dijkstra寻路结束后，我们遍历一遍终点节点的所有状态，找到一个最小的dis[ed][i]，即最优解

int ans = 1e9;
for (int i = 0; i <= k; i++) ans = min(ans, dis[ed][i]);

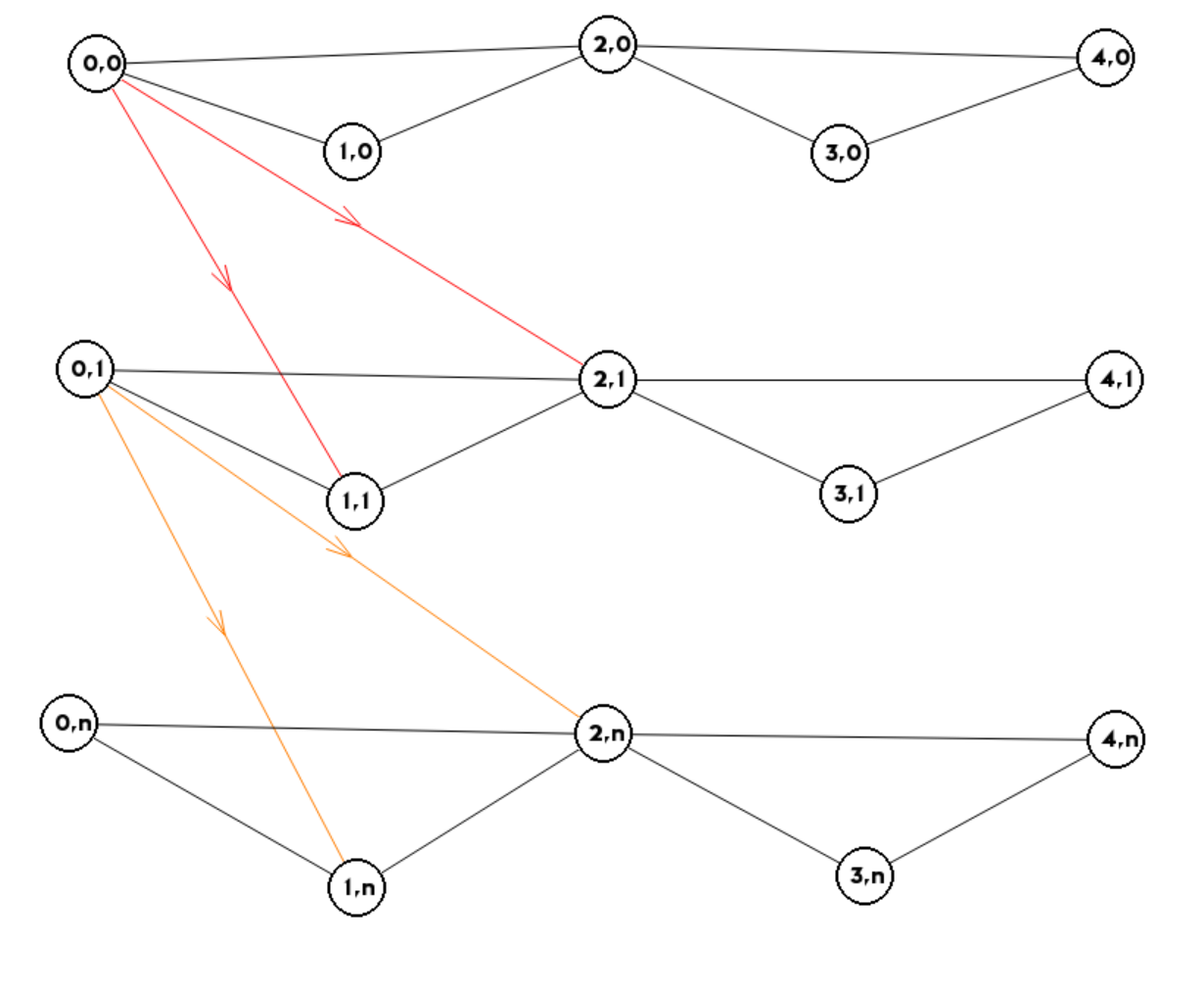
图上的每一个节点都有向下层的可联通节点前进的无权边（免费）

上图以 $0$ 号节点为例，它可以通过免费次数构建出来的边向下层图移动，直到免费次数用尽

总而言之，解决分层图的关键就在建图，需要正确地通过不同的状态构造出图

完整代码：

#include <vector>
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
#define streampreset() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
using namespace std;

struct edge
{
    int v, w;
};

struct node
{
    int dw, dnode, cnt;
    bool operator<(const node& a)const {
        return dw > a.dw;
    }
};

int n, m, k;
int st, ed;
vector<edge> e[50010];
priority_queue<node> q;
int dis[20010][12];
bool vis[20010][12];

void insert(int u, int v, int w) {
    e[u].push_back({ v,w });
}

void init(void) {
    memset(dis, 0x3f, sizeof dis);
}

void dijkstra(int st) {
    init();
    q.push({ 0, st, 0 });
    dis[st][0] = 0;
    while (q.size())
    {
        const node ttop = q.top();
        q.pop();
        if (vis[ttop.dnode][ttop.cnt]) continue;
        vis[ttop.dnode][ttop.cnt] = 1;
        for (auto it = e[ttop.dnode].begin(); it != e[ttop.dnode].end(); it++) {
            if (ttop.cnt < k&& dis[it->v][ttop.cnt + 1] > dis[ttop.dnode][ttop.cnt]) {
                dis[it->v][ttop.cnt + 1] = dis[ttop.dnode][ttop.cnt];
                q.push({ dis[it->v][ttop.cnt + 1],it->v,ttop.cnt + 1 });
            }
            if (dis[it->v][ttop.cnt] > dis[ttop.dnode][ttop.cnt] + it->w) {
                dis[it->v][ttop.cnt] = dis[ttop.dnode][ttop.cnt] + it->w;
                q.push({ dis[it->v][ttop.cnt],it->v,ttop.cnt });
            }
        }
    }
}

int main()
{
    streampreset();
    cin >> n >> m >> k >> st >> ed;
    int u, v, w;
    for (int i = 0; i < m; i++) {
        cin >> u >> v >> w;
        insert(u, v, w);
        insert(v, u, w);
    }
    dijkstra(st);
    int ans = 1e9;
    for (int i = 0; i <= k; i++) ans = min(ans, dis[ed][i]);
    cout << ans;
    return 0;
}