Dijkstra单源最短路朴素算法
基于无优化的朴素算法,这里使用邻接矩阵的方法存储路径(空间复杂度高)
Dijkstra单源最短路的算法原理如下:
从起始点s开始,每次依据贪心选取最近连通点且未被访问过的点,移动到该点上,更新最短路径,直到把所有点都访问完
初始化时,需要将s起始点到所有点的dis[i]距离,赋值为极大值,表示不能连通从s出发
for (int i = 0; i <= n; i++)
dis[i] = 1e9;枚举当前能连通的所有点,记录最短路径点min_node(初始化为0),如果不能更新最短路径点,则说明遍历完了所有的点
有:
if (min_node == 0) break;并对其进行标记,表示以及被访问过了
vis[min_node] = 1;遍历所有点,更新最短路径:
for (int i = 1; i <= n; i++)
if (dis[i] > dis[min_node] + g[min_node][i])
dis[i] = dis[min_node] + g[min_node][i];//如果当前点可以组成更短的路径,那就更新
//或写成
for (int i = 1; i <= n; i++)
dis[i] = min(dis[i], dis[min_node] + g[min_node][i]);
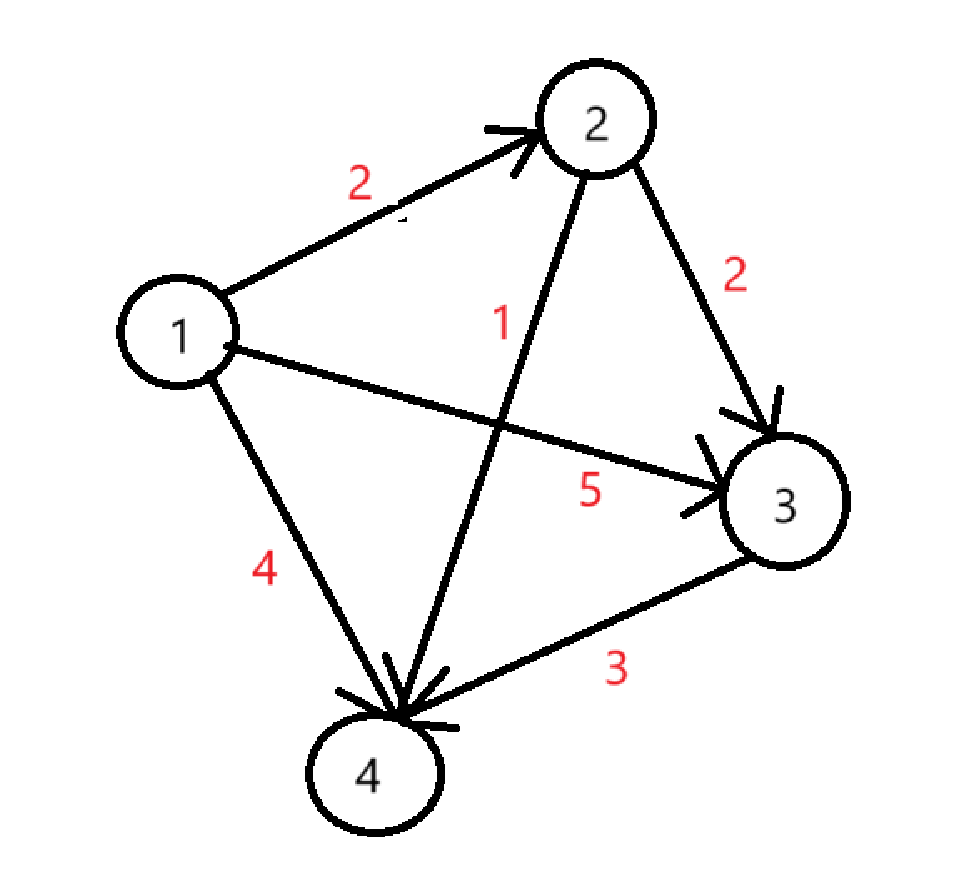
以上图为例:有参数如下
4 6 1 // 四个节点,六条边,从一号点开始
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4我们来逐步推导一遍
初始化:dis[]={1e9, 0, 1e9, 1e9, 1e9}
第一轮:
遍历所有未访问的点,$1$号点到自身的路径为 $0$,为最短,min_node为$1$
标记$1$号点,接着遍历所有节点并更新路径为:dis[]={1e9, 0, 2, 5, 4}
第二轮:
遍历所有未访问的点,$2$号点到$1$号点的路径为 $2$,为最短,min_node为$2$
标记$2$号点,接着遍历所有节点并更新路径为:dis[]={1e9, 0, 2, 4, 3}
第三轮:
遍历所有未访问的点,$4$号点到$1$号点的路径为 $3$,为最短,min_node为$4$
标记$4$号点,接着遍历所有节点并更新路径为:dis[]={1e9, 0, 2, 4, 3}
第四轮:
遍历所有未访问的点,$3$号点到$1$号点的路径为 $4$,为最短,min_node为$3$
标记$4$号点,接着遍历所有节点并更新路径为:dis[]={1e9, 0, 2, 4, 3}
第五轮:
遍历所有未访问的点,可以发现所有的点都被遍历过了,于是退出循环
Dijkstra是一种基于贪心的最短路径算法,但是他不能处理存在负边权的情况,这是因为如果存在负权边,那就有可能先通过不是距起始点最近的一个次优点,再通过这个负权边,使得路径之和更小
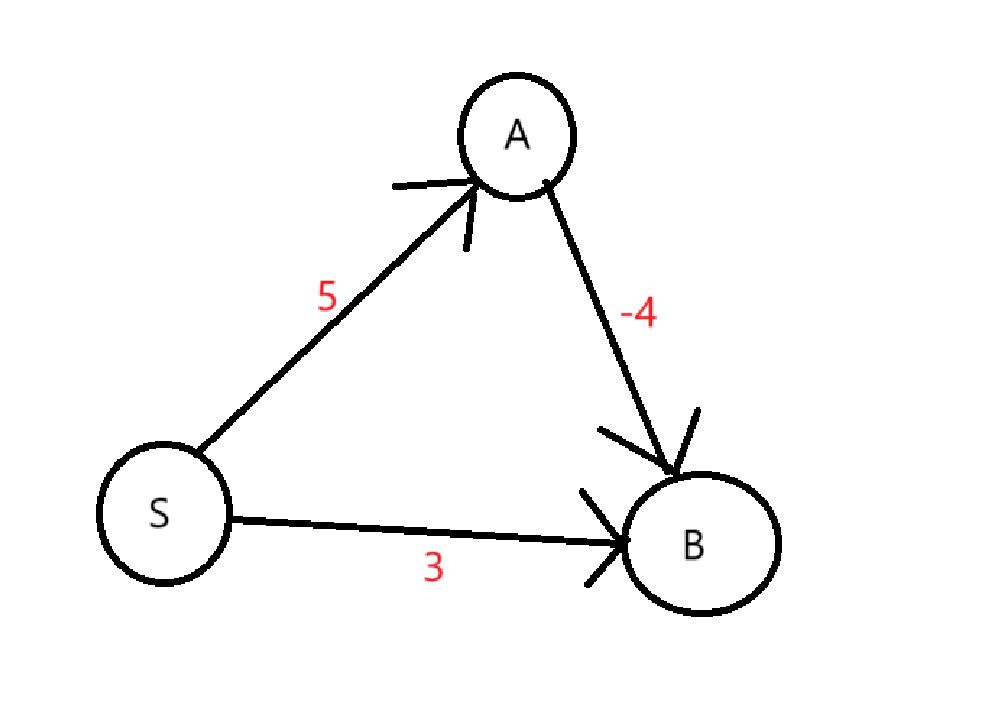
如上图所示,从S点出发,贪心会选择S -> B,而不是全局最优的S -> A -> B,这就发生了错误
- 贪心的正确性这里不做赘述,详情可自行查看:
朴素算法如下:
bool vis[N];
int dis[N];
int g[N][N];//邻接矩阵存储路径
void dijkstra(int s) {
for (int i = 0; i <= n; i++)
dis[i] = 1e9;//赋值极大值
dis[s] = 0;//起始点被访问过
while (true)
{
int min_node = 0, min_mem = 1e9;
for (int i = 1; i <= n; i++) {
if (!vis[i] && min_mem > dis[i])
{
min_node = i;
min_mem = dis[i];
}
}//找到最短路径点,记录编号
if (min_node == 0) break;
vis[min_node] = 1;
for (int i = 1; i <= n; i++)
if (dis[i] > dis[min_node] + g[min_node][i])
dis[i] = dis[min_node] + g[min_node][i];
}
}基于使用邻接表存储连接边的方法,可以有效的降低空间复杂度
在稀疏图(边的数量远小于顶点数量平方的图)中,邻接矩阵会大量占用无用的内存,导致Re,我们采用邻接表的办法,只存储存在的边,减少无关占用。相反,在稠密图(边的数量接近顶点数的平方的图)中,邻接表会遍历一整条链,检索时间会大大增加(不做优化),我们就采取邻接矩阵的方法来存储,每次只需要通过下标快速检索
通过结构体和vector来构造边的链表
struct edge
{
int v, w;//v表示连接到的节点,w表示边权重
};
vector<edge> e[10010];插入边操作
void insert(int u, int v, int w) {
e[u].push_back({ v,w });
}
cin >> u >> v >> w;
insert(u, v, w);然后是使用朴素的Dijkstra算法实现单源最短路
void dijkstra(int s) {
memset(dis, 0x3f, sizeof dis);//初始化可以使用memset 0x3f 批量操作
dis[s] = 0;//起始点被访问
for (int i = 1; i <= n; i++) {
int min_node = 0;//初始化
for (int j = 1; j <= n; j++)//遍历所有点
min_node = dis[j] < dis[min_node] && !vis[j] ? j : min_node;
//找未被访问过的点中的最近点,判断最小值
if (!min_node) break;//如果没能找到,即min_node未更新,退出循环
vis[min_node] = 1;//当前点已被访问过
for (auto it = e[min_node].begin(); it != e[min_node].end(); it++)//迭代器遍历当前点的所有连通边
dis[it->v] = min(dis[min_node] + it->w, dis[it->v]);//更新最小值
}
}使用迭代器遍历时,需要通过箭头运算符 -> 来访问结构体的成员元素
for (auto it = e[min_node].begin(); it != e[min_node].end(); it++)
dis[it->v] = min(dis[min_node] + it->w, dis[it->v]);同样也可使用C++11标准内的区间遍历
for (auto iter : e[min_node])
dis[iter.v] = min(dis[min_node] + iter.w, dis[iter.v]);区间遍历的一般格式
for (dataType rangeVariable : array) dataType为需要遍历的数组的数据类型, rangeVariable为循环内范围变量的名称,该变量用来接收遍历元素的值,array为需要遍历的数组名,区间遍历的范围变量只需要通过 . 就能访问结构的成员元素
评论区(暂无评论)